How to Solve a Logarithmic Equation for x
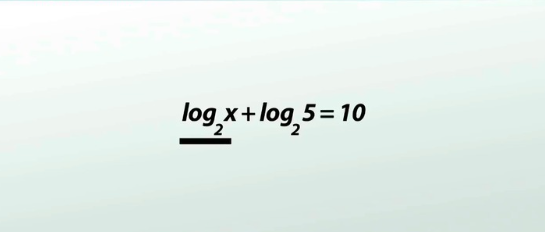
Logarithmic equations are frequently encountered in algebra and advanced mathematics. These equations help describe processes such as exponential growth, decay, and scaling. Whether you’re a student, teacher, or math enthusiast, understanding how to solve a logarithmic equation for x is essential for mastering algebraic concepts.
This article presents a comprehensive guide to solving logarithmic equations for the variable x, covering basic principles, types of equations, and step-by-step strategies with examples.
Understanding Logarithmic Equations
For example:
log₂(8) = 3 means 2³ = 8
Logarithmic equations typically come in these forms:
- log_b(x) = y
- log_b(f(x)) = log_b(g(x))
- a·log_b(x) + c = d
Solving such equations usually means isolating x using logarithmic properties or converting to exponential form.
Important Logarithmic Rules
- Product Rule: log_b(mn) = log_b(m) + log_b(n)
- Quotient Rule: log_b(m/n) = log_b(m) – log_b(n)
- Power Rule: log_b(mⁿ) = n·log_b(m)
- Change of Base: log_b(a) = log_c(a)/log_c(b)
- Inverse Rule: log_b(b^x) = x and b^(log_b(x)) = x
These rules allow for simplifying, combining, or rewriting logarithmic expressions.
General Strategy
When solving any logarithmic equation for x, follow these steps:
- Identify the type of logarithmic equation.
- Isolate the logarithmic term(s).
- Simplify using logarithmic rules if needed.
- Convert to exponential form.
- Solve the resulting equation algebraically.
- Check for extraneous solutions by ensuring all expressions inside the logs are positive.
Example 1: Basic Logarithmic Equation
log₅(x) = 2
Step 1: Convert to exponential form
x = 5²
Step 2: Solve
x = 25
This is a simple one-step conversion. The logarithm is already isolated, making it quick to solve.
Example 2: Logarithmic Equation with Coefficient
2·log₃(x) = 4
Step 1: Divide both sides by 2
log₃(x) = 2
Step 2: Convert to exponential form
x = 3²
Step 3: Solve
x = 9
Again, isolate the log, then exponentiate.
Example 3: Multiple Logarithms on One Side
log₁₀(x) + log₁₀(x – 4) = 1
Step 1: Use the product rule
log₁₀(x(x – 4)) = 1
Step 2: Simplify the expression
log₁₀(x² – 4x) = 1
Step 3: Convert to exponential form
x² – 4x = 10¹ = 10
Step 4: Solve quadratic
x² – 4x – 10 = 0
Use the quadratic formula:
x = [4 ± √(16 + 40)] / 2 = [4 ± √56] / 2
x = [4 ± 7.48] / 2
x ≈ 5.74 or -1.74
Step 5: Check for validity
- For x ≈ 5.74, both log arguments are positive ✅
- For x ≈ -1.74, log(x) is undefined ❌
Valid solution: x ≈ 5.74
Example 4: Equation with Logarithms on Both Sides
log₂(x + 3) = log₂(2x – 1)
x + 3 = 2x – 1
Step 2: Solve
3 + 1 = 2x – x → x = 4
Step 3: Check
- log₂(4 + 3) = log₂(7)
- log₂(8 – 1) = log₂(7) ✅
So, x = 4 is correct.
Example 5: More Complex Case
Step 1: Use the quotient rule
log₄((x – 1)/(x + 2)) = 1
Step 2: Convert to exponential form
(x – 1)/(x + 2) = 4¹ = 4
Step 5: Check
- log₄(-3 – 1) is log₄(-4), which is undefined ❌
No valid solution. No real solution exists for this equation.
Dealing with Natural Logarithms
Natural logarithms (ln) are simply logarithms with base e ≈ 2.71828.
Example 6:
ln(x – 5) = 3
Step 1: Convert to exponential form
x – 5 = e³
Step 2: Approximate
x = e³ + 5 ≈ 20.085 + 5 = 25.085
So, x ≈ 25.085
Using Substitution Method
Sometimes substitution can help simplify a difficult equation.
Example 7:
log₁₀(x² + 4x + 4) = 2
Recognize that x² + 4x + 4 = (x + 2)²
So:
log₁₀((x + 2)²) = 2
Use power rule:
2·log₁₀(x + 2) = 2
Divide both sides:
log₁₀(x + 2) = 1
Check: log₁₀(8² + 4*8 + 4) = log₁₀(64 + 32 + 4) = log₁₀(100) = 2 ✅
Valid solution: x = 8
When No Solution Exists
Always be aware that logarithms are undefined for zero or negative arguments.
Tips for Solving Logarithmic Equations
- Always isolate the logarithmic term first.
- Be cautious with domain restrictions. Ensure arguments are always greater than zero.
- Use logarithmic properties to combine or simplify terms before converting to exponential form.
- Avoid rounding too early. Keep calculations exact until the final answer.
- Verify answers. Substituting back helps confirm your solution is valid.
Real-Life Applications
Logarithmic equations are not just theoretical. They are used in:
- Earthquake measurement (Richter scale)
- Sound intensity (decibels)
- Banking and interest calculations
- Chemical concentration (pH levels)
- Computer algorithms (data compression, complexity analysis)
Knowing how to solve a logarithmic equation for x equips you for tackling these real-world challenges.
Final Thoughts
With a good grasp of the rules, properties, and problem-solving steps, these equations become far less intimidating. Practice regularly, double-check your work, and soon you’ll master any logarithmic challenge thrown your way.